What if you were observing a geometric shape that looks familiar, yet behaves unlike anything you’ve ever encountered. As it rotates, it seems to defy physics and reality as you know it. It inflates and deflates, warps into itself, implodes and explodes. You think to yourself “This is impossible!” This is the exact experience I had in high school, and it has stayed with me to this day. It was the first time I saw a visualization of a four dimensional object, a tesseract:

A tesseract is a hypercube—a cube that extends to the fourth dimension. I didn’t understand it much then, and still don’t quite grasp it now. How can something in the fourth dimension exists? How can we even try to visualize it? How do we even know what it looks like? What else is the fourth dimension? Is there even higher dimensions? These are all questions I’ve asked myself over the years and I want to share how I currently perceive those dimensions. I want to share how I understand higher dimensions and what it means for the universe. I also want to raise certain important philosophical inquiries that questions the nature of reality.

Seeing the Unseen

Here is the challenge: we live in a three dimensional world. In our world, we perceive objects with length, width, and depth. Our brains have evolved to thrive in this three dimensional world. Our sense and intuition work well for this world. Intuitively, we can easily visualize and understand a point, a line, a square, and a cube in space. These are shapes that are familiar to us and what makes up our geometrical three dimensional world. So, how do we progress from these easily recognizable shapes to a object like the tesseract? Let me walk you through each of the dimensions and show you how each becomes an extension of the previous.

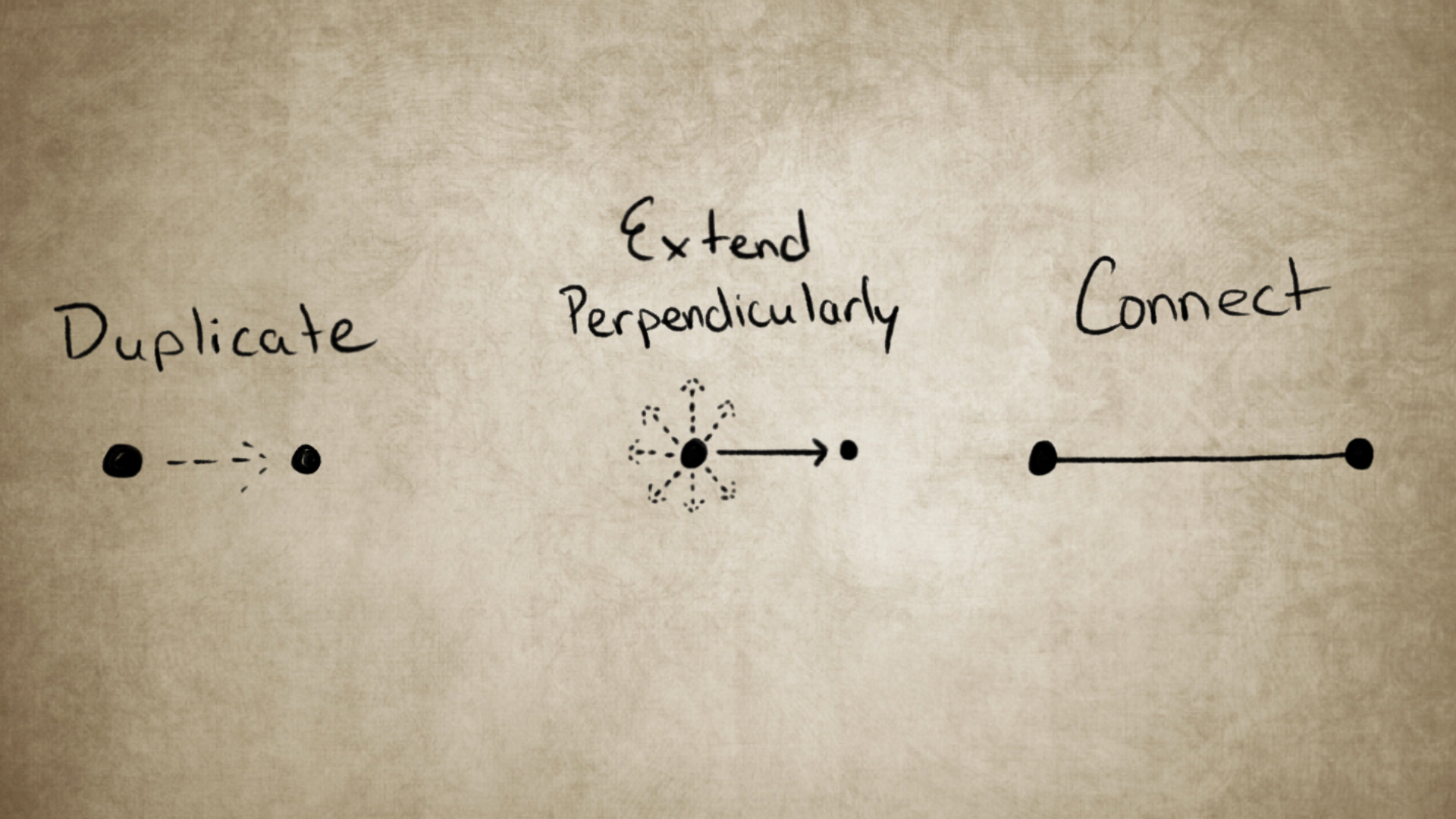
Let’s begin in the 0th dimension—a single point in space. A point does not have length, width, or depth. It is pure location, without any extension. To reach the 1st dimension, we must take the point, duplicate it, extend it perpendicularly, and connect them. This is the fundamental procedure that we will be using as we continue to extend to higher dimensions. First, duplication is an easy concept to understand: we simply replicate the current form, the point, to obtain two of them. Next, and the most important step to grasp, is the perpendicular extension. Now, for a point, this makes little sense; what is perpendicular to a point? Well, any direction is equally valid in this sense. Thus, choose any direction from the initial point, extend the duplicated point, and connect the two. Now, we have the first dimension: a line. In this dimension, we gain length.

Moving on to the 2nd dimension. Following the same procedure, we want to duplicate the line, then extend it perpendicularly. Now, the second step becomes much more relevant to the procedure. A line has perpendicularity, specifically at a 90 degree angle. This is the direction we must extend the duplicated line. If we extend it by the length of the line itself, and connect each end, we gain another similar shape: a square. A square, or any two dimensional object, has both length and width.

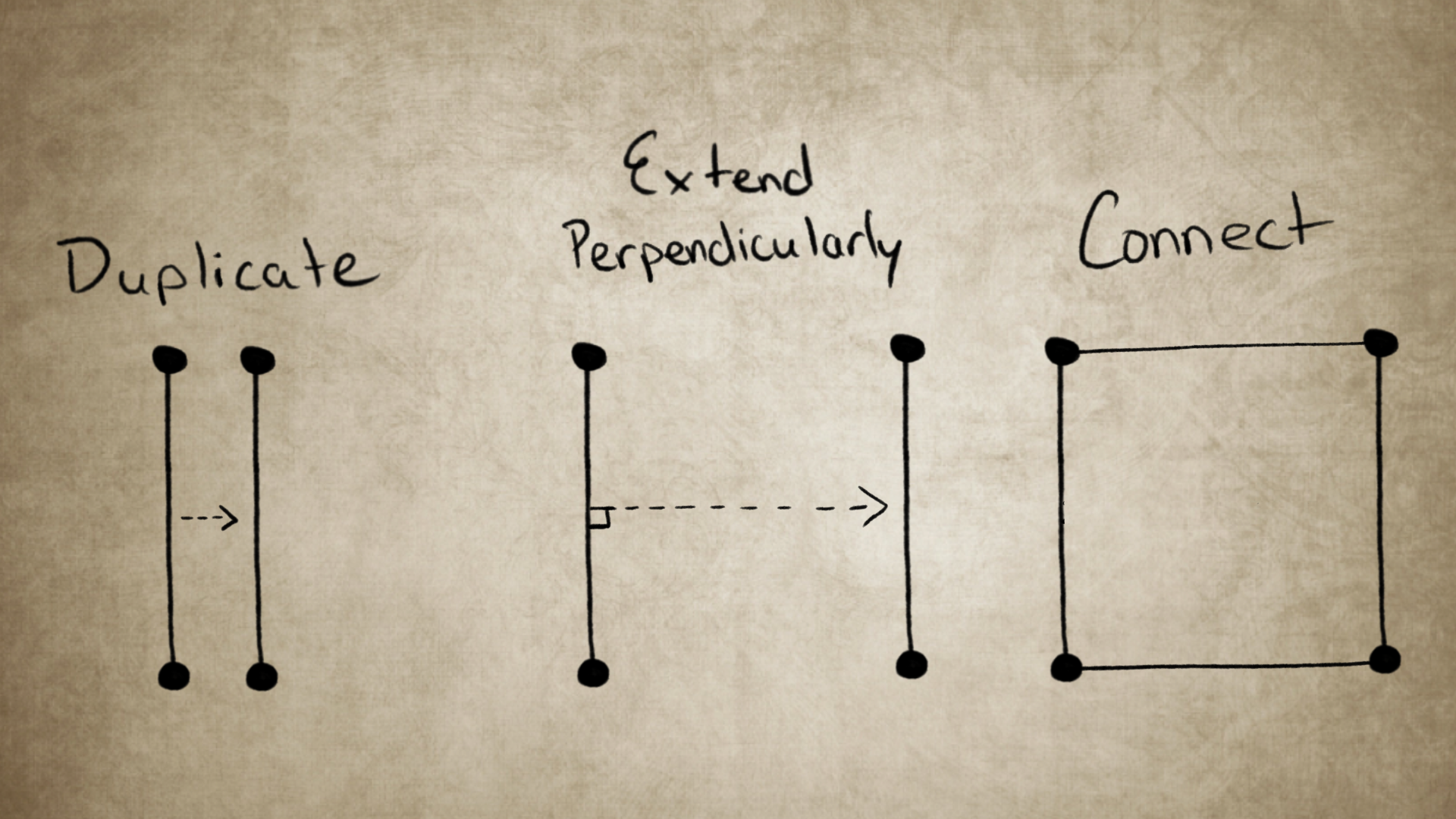
Continuing to the 3rd dimension, let’s duplicate our square. Next, let’s extend it perpendicular to the plane of the square. Once again, if extend it by the amount of the length or width of the square and connect each corner to get a cube. A cube is three dimensional because it has length, width, and depth.

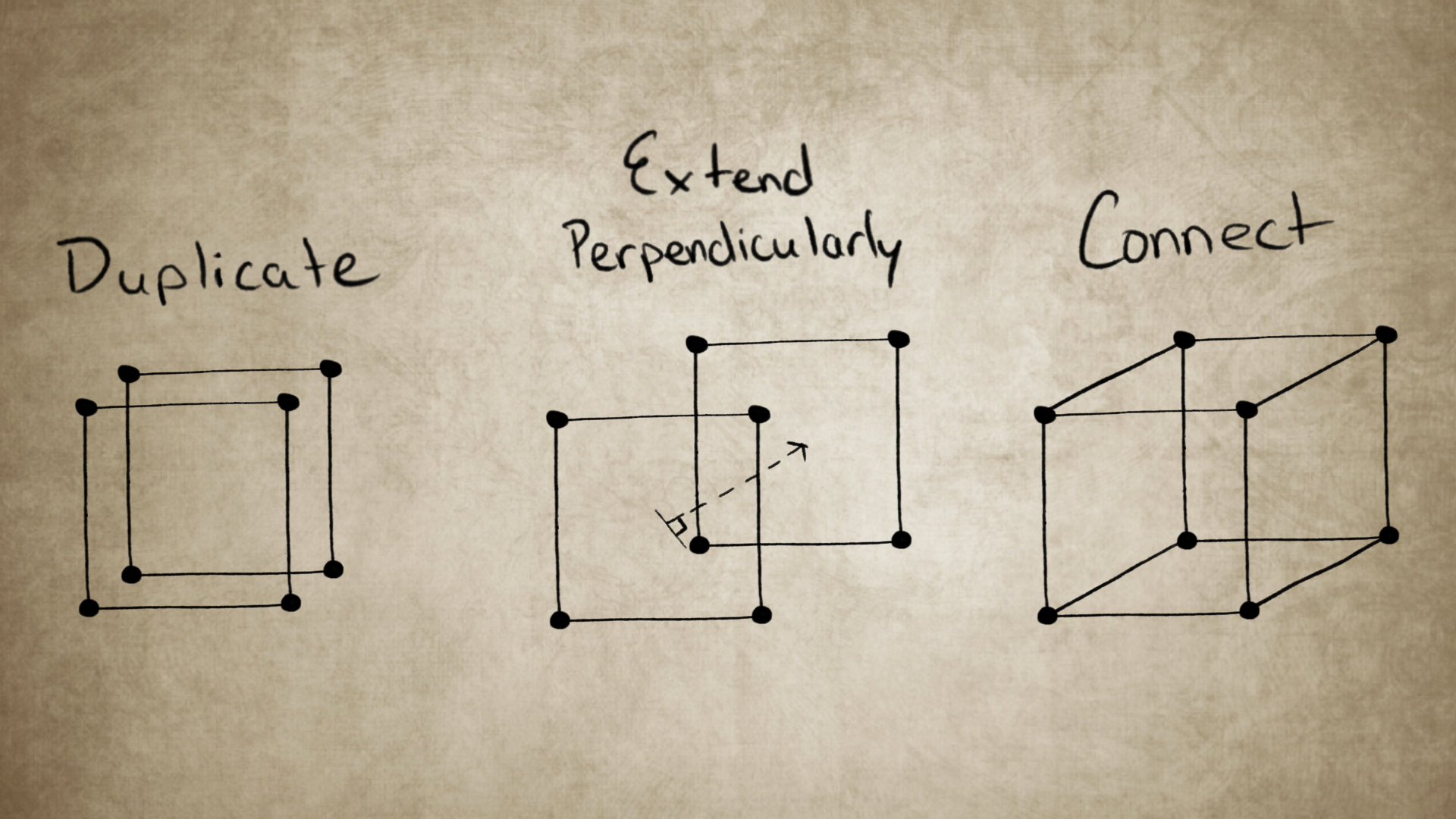
For each new dimension, we duplicate, we extend perpendicularly, and we connect. This is the same procedure we are going to use to understand the fourth dimension. Continuing, let’s take our cube, duplicate it, and extend it perpendicularly. Then, if we extend it at a length equal to either length, width or depth of the cube and connect the two at each of the four corners, we have a hypercube, or tesseract!

Easy right? Well, actually this is where it gets complicated. Even though we understand the steps and implemented them correctly, there is one question we didn’t ask: how do we extend a cube perpendicularly? This is where our intuition dissolves. What is perpendicular to depth? We have no intuition or experience of this. It is similar to asking us to taste colours or smell sound. It is beyond our senses and experiences. However, mathematically, we can do it and visualize it. Mathematics isn’t bound by our three dimensional perception or limitations. But we are. We have no real intuition on what we are seeing.

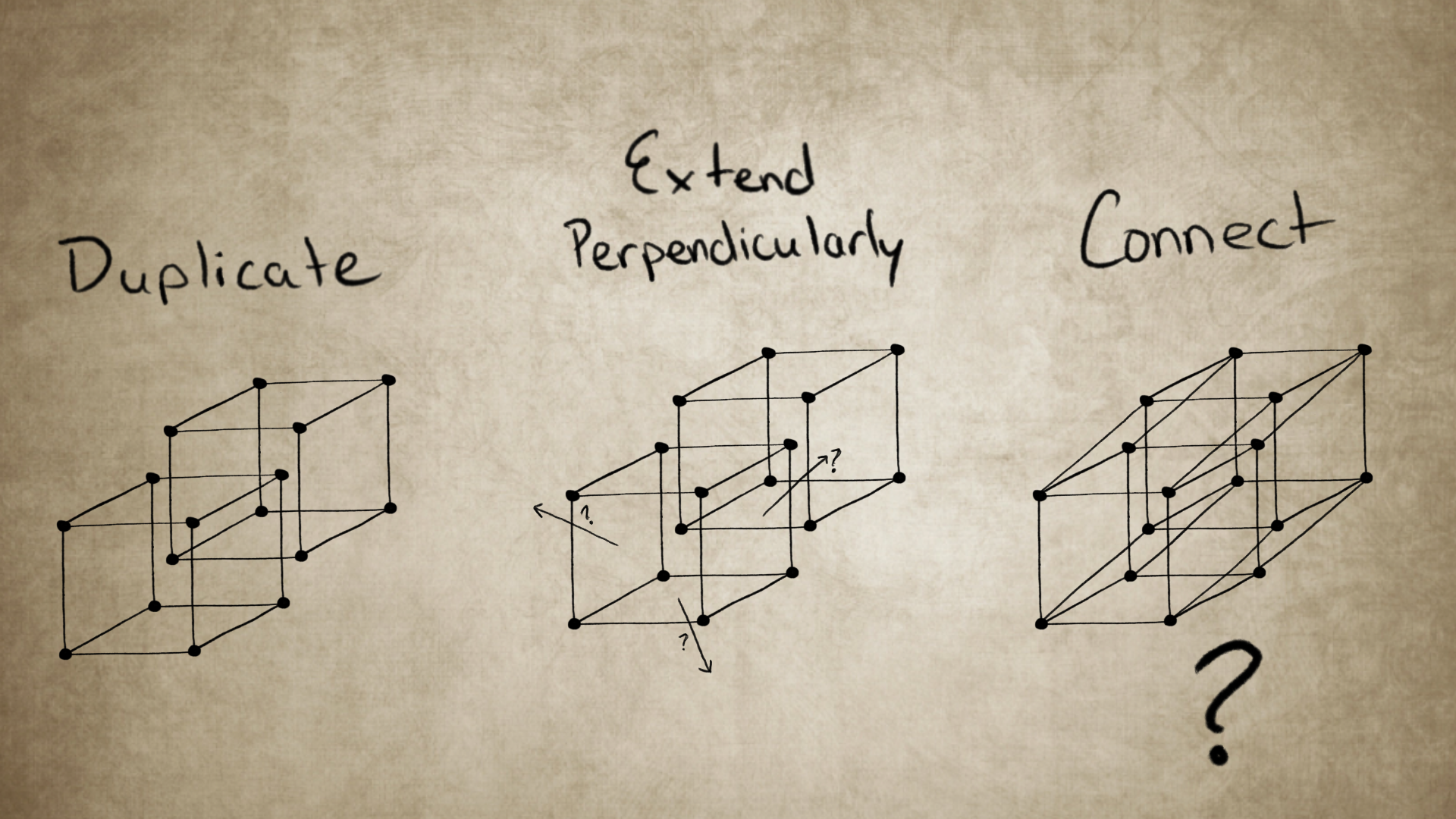
So, instead of trying to brute-force our way into understanding, let’s take a step back and build on intuition we do have. Let’s examine a simpler world, a flat one, and try to understand their limitations.

Looking Up From Below

Let’s imagine we are observers of another world that is only two dimensional. In this world, there is no up or down, only left and right, forward and back. This is the world of Flatland, a thought experiment introduced by Edwin Abbott Abbott in 1884.

For Flatlanders, shapes like squares and circles are familiar. But the concept of “depth” is nonsense to them. It’s not just unimaginable, its unconceivable. Now, let’s imagine what happens when a three dimensional object enters their world.

Take a sphere passing through Flatland. At first, the Flatlanders would see only a single point for an instant. That point would grow into a circle, expand wider and wider, then shrink again before vanishing completely. What we know is simply a sphere intersecting their two-dimensional plane. But to them, it would look like a series of strange, impossible transformations. How could a point appear out of nowhere, grow from nothing, and then disappear?

Now imagine a cube passing through their world. This would be even more bewildering. Depending on the angle, they might see a square suddenly appear and vanish, or a shape that twists and morphs in ways that make no sense at all as the cube rotates.

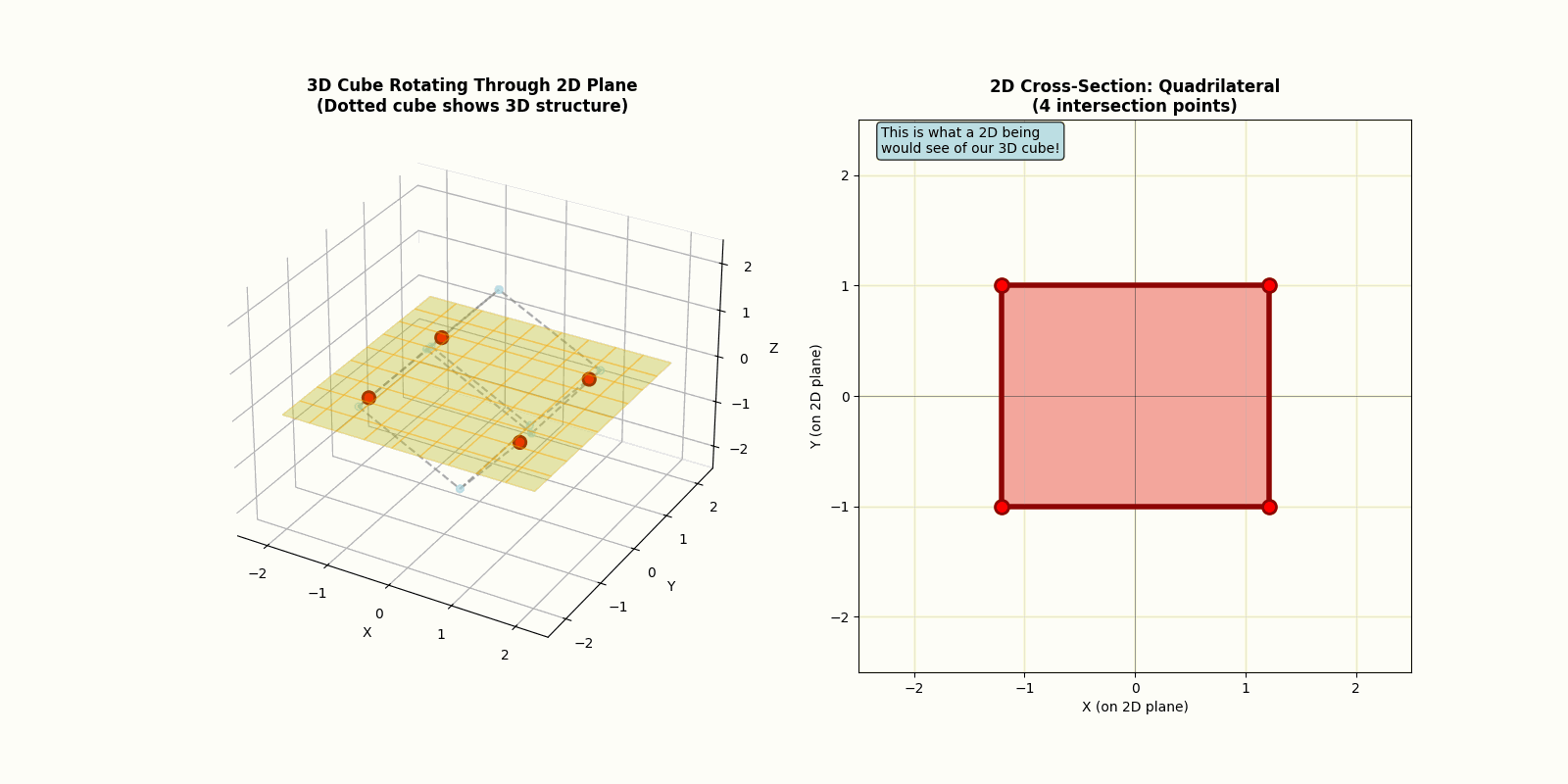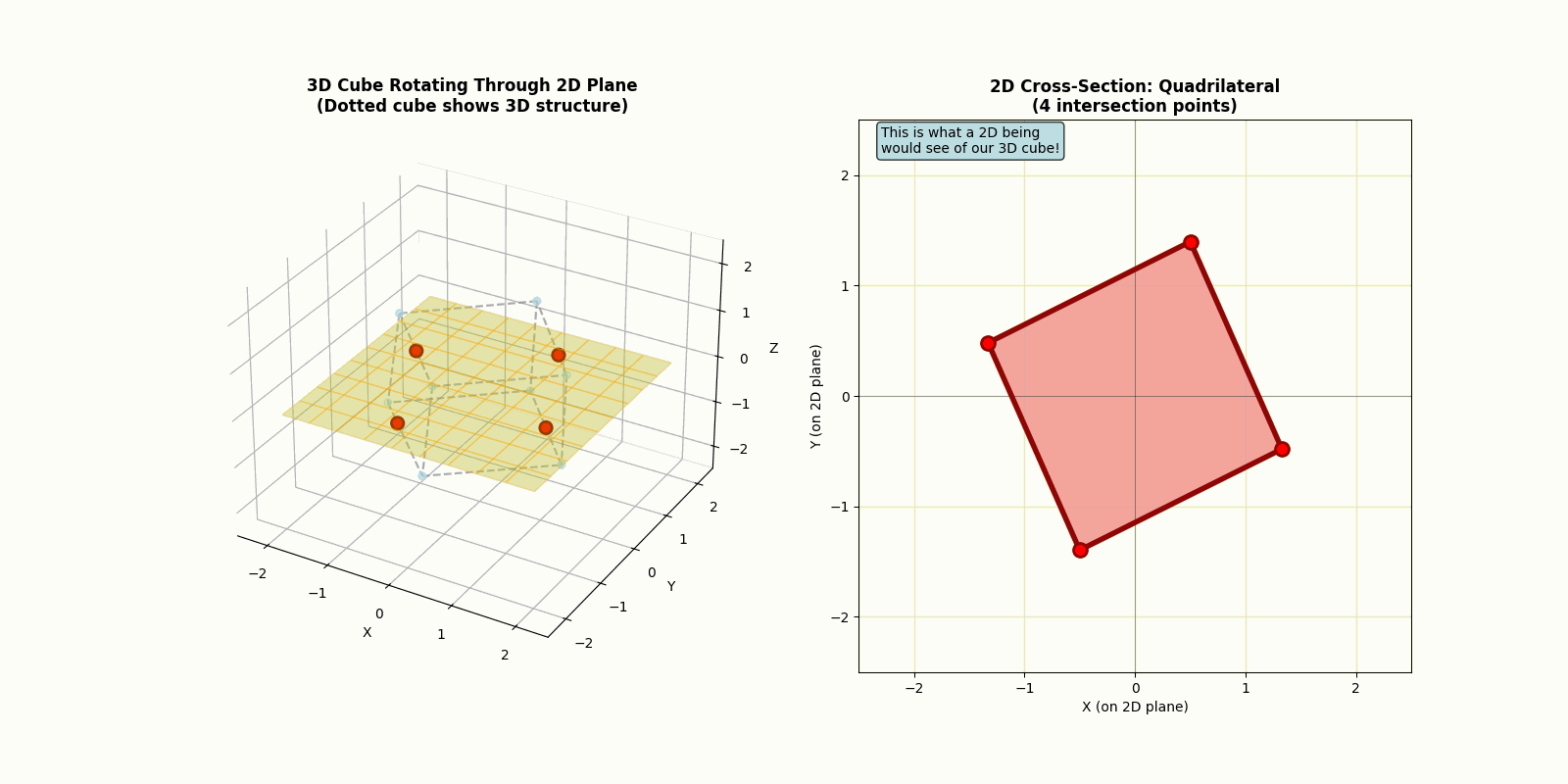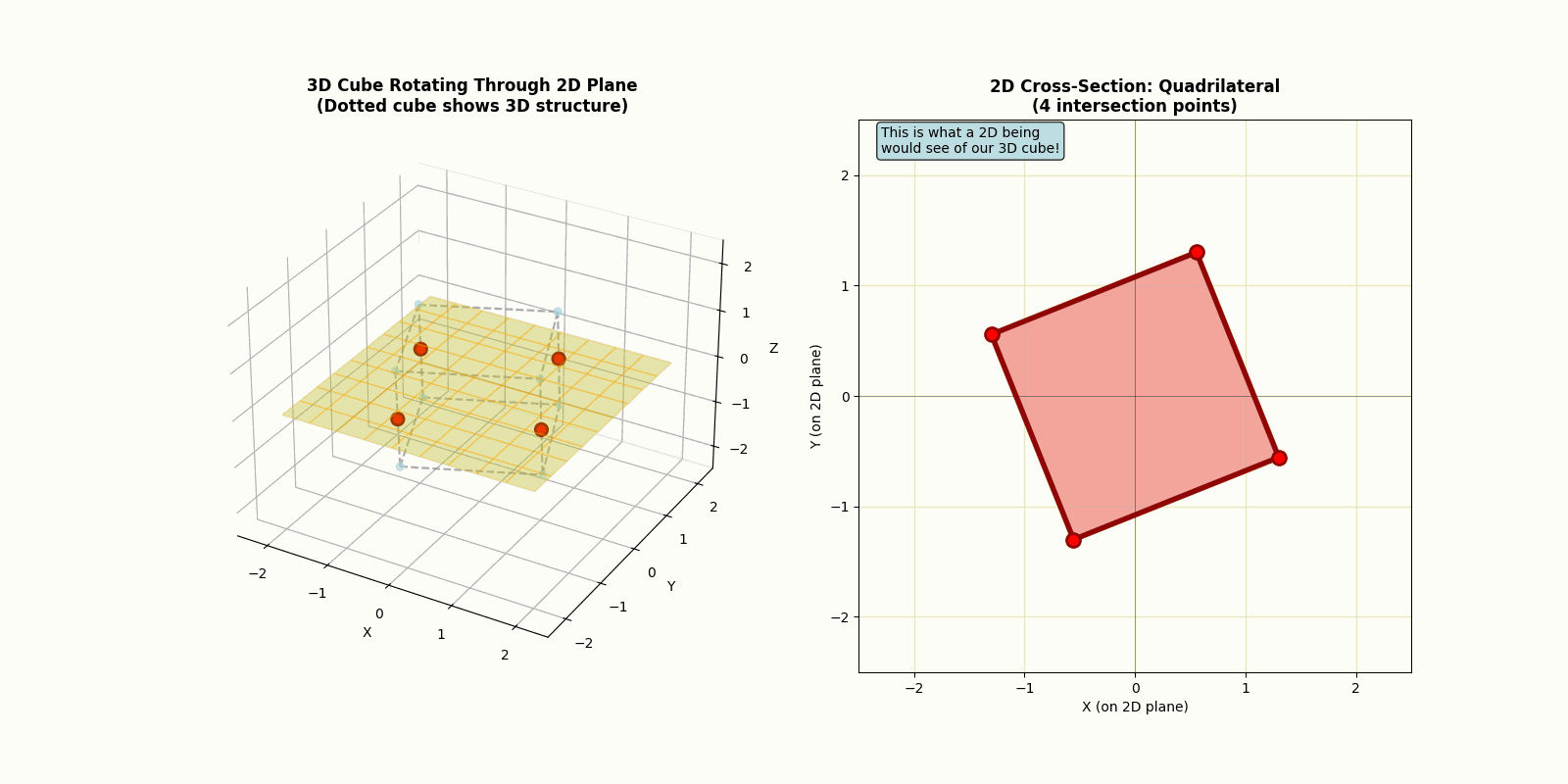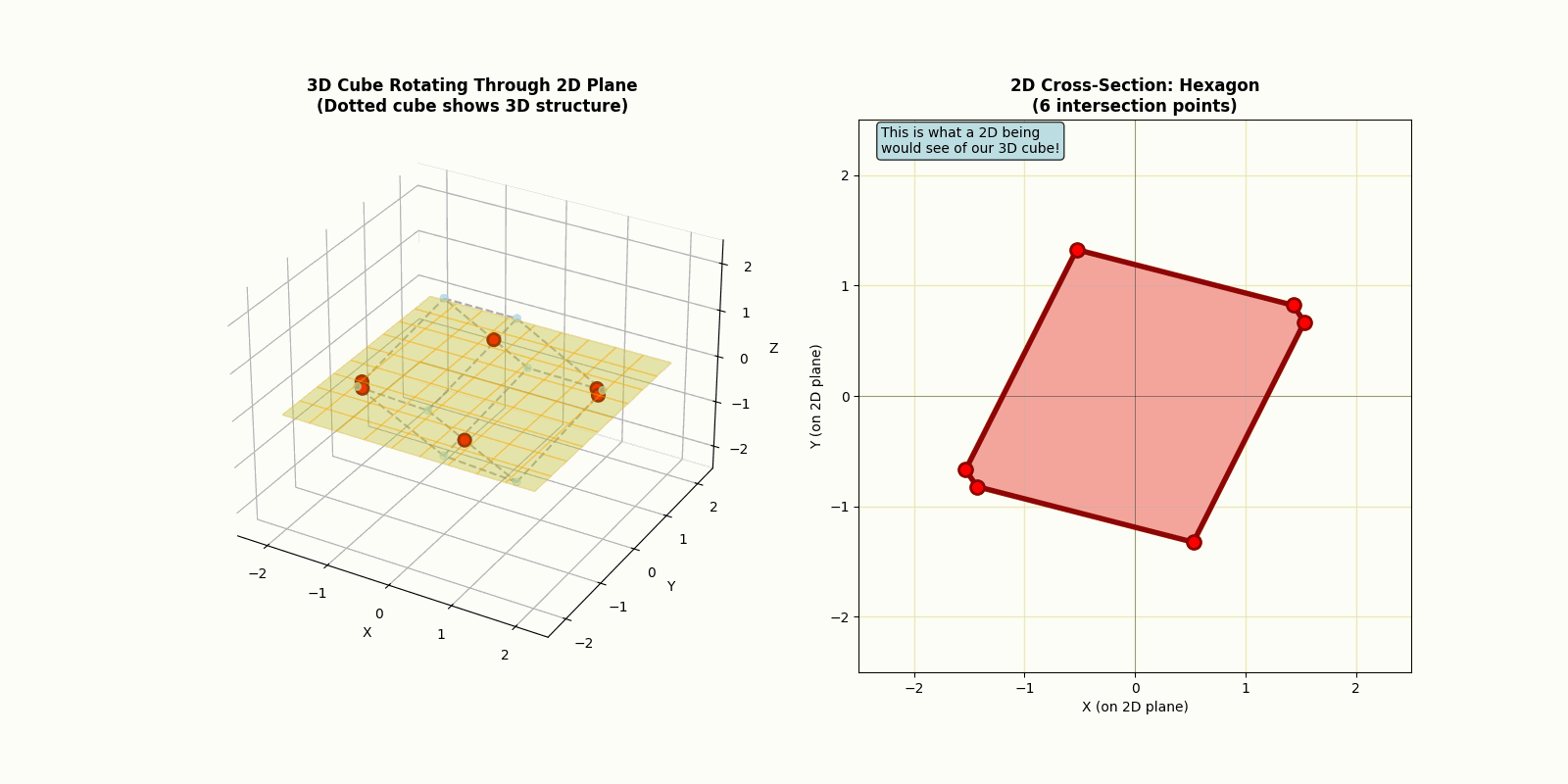
They have no concept of what really happened. But we, as three-dimensional beings, understand perfectly what occurred. We see the full object and how they intersect with their plane. However, as a four dimensional objects enter our world, we would be just as confused. A hypersphere that enters our world would appear as a sphere that grow from nothing, shrinks, and disappears. A tesseract would fold into itself and explode outwards as it rotates.

Similar to the Flatlanders only perceiving the two dimensional slice of the three dimensional object, we would only perceive a three dimensional cross-section of the four dimensional object. We are Flatlanders too, just with an additional dimension. This concept is crucial to grasp as we step further into the fourth dimension. We only see slices of higher realities, which leads us to one of the most profound shifts in physics: the fourth dimension isn’t just space, it’s time.

Time, the Perpendicular Axis We Don’t Notice

Einstein revolutionized physics with his paradigm shifting theory of relativity. He discovered something astonishing: space and time are not separate. In fact, they are woven together into a single four-dimensional fabric called “spacetime”.

In the world we perceive, we have length, width, depth, and time. Time is the perpendicular axis we don’t think about. Time isn’t perpendicular in a geometric sense we can visualize, but in a physical sense. It is a dimension independent from the three spatial ones, yet deeply intertwined with them.

Let’s think of a particle in the universe. Over time, each particle traces a path through spacetime called a world line. A world line is a record of everywhere the particle has been in space, where it is going, and at what given time. Humans trace something thicker. Our entire life, from birth to death, is a single continuous structure in spacetime. However, we don’t perceive this world line. We only experience a thin slice of it the flows with time, the now.

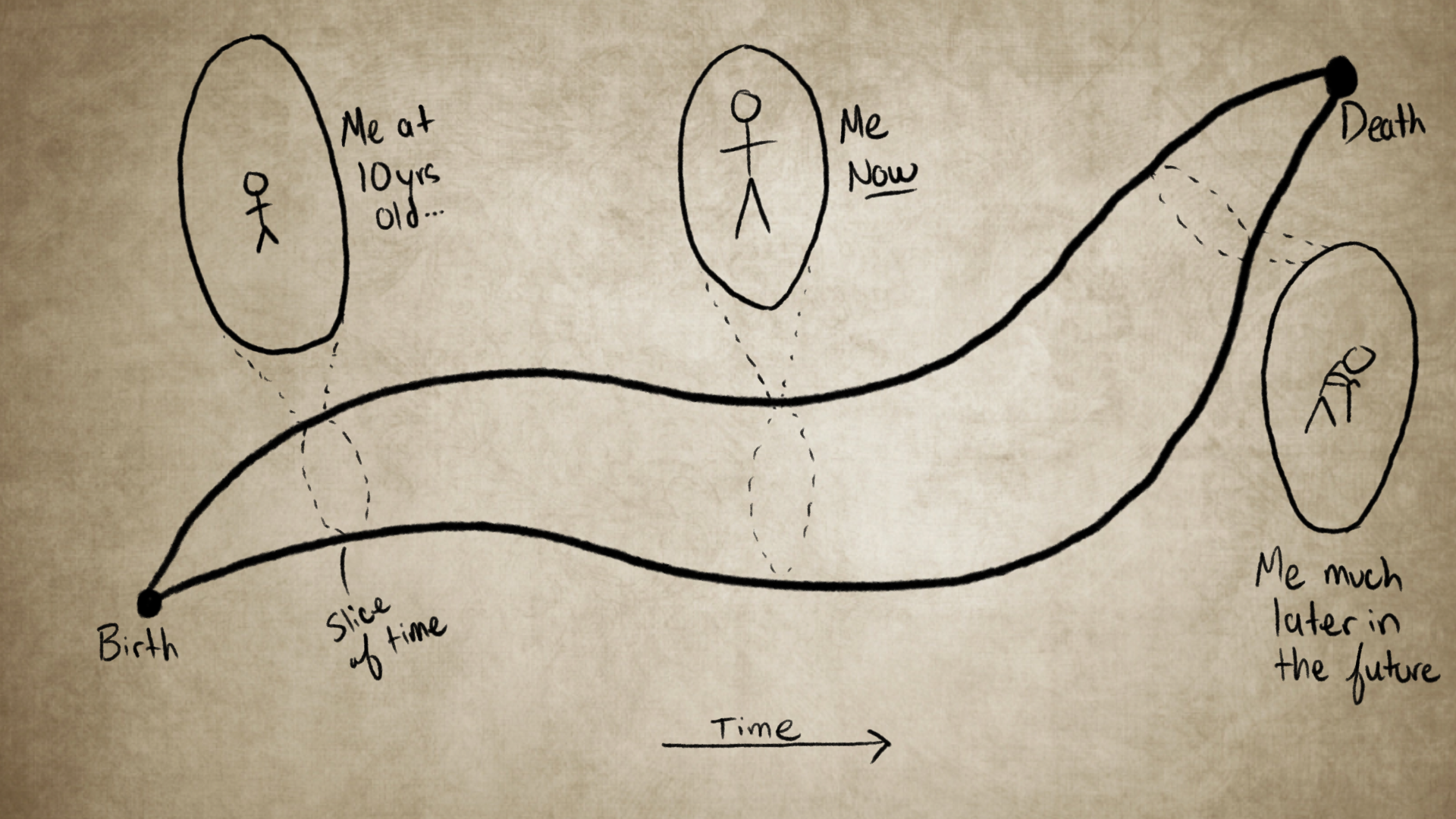
Just as Flatlanders experienced a slice of a three dimensional object, or us experiencing a three dimensional slice of the tesseract, we see a three dimensional slice of a spacetime object, a single moment, called the “present”. A being that could perceive four dimensions directly would see our whole existence laid out at once. Our first breath, our final breath. Every choice, every heartbeat, as a single sculpture woven into the fabric of spacetime.

This breakthrough in our understanding of the universe is still up for debate and discussion. However, if it is true, then what does that mean about us? This idea leads us to a deep philosophical puzzle—is our fate already planned out then?

Is the Future Already Written?

The philosophical notion known as “eternalism” is a concept which describes all time, past, present, and future, exist simultaneously. Just as every part of the cube exist at once when intersecting Flatland, every moment of the universe exists as well.

If this is true, then your entire life is already carved into spacetime. Every moment and decision you’ve made and will make is already imprinted in the universe. This concept can be unsettling because it raises significant questions: “Is free will an illusion?” Well, not necessarily. In fact, some philosophers argue the philosophy of “presentism”, where only the present exists, the past and future does not. We can take this a step further. I believe that some aspects of eternalism and presentism can co-exist; they are simply describing different perspectives.

Let’s imagine that the fourth dimension does exist. A being that can observe our universe from a fourth dimensional perspective will see our entire universe timeline at once. Every particle that has been and where it was. It would also see the world line of every human that ever was, from start of humanity, to its end. From this point of view, time isn’t something that flows, it simply is. Everything that could happen has already happened. This fourth dimensional being is not bound to the shackles of the flow of time.

Imagine a being that time doesn’t flow. How can we even start to understand what this means? Thinking about this is difficult, believe me, I tried. But if we go back to the Flatland analogy, Flatlanders ask the same question “How is there more than the shape we perceive?” If they only see a cross section of a sphere, and are told, the entire sphere exists simultaneously, including the cross section, they would be dumbfounded. And so are we when we think of perceiving time not as cross sections.

However, since time isn’t a geometrical object, it get’s much weirder. Movement, processing, propagation, thinking, etc., all rely on the flow of time. If there is no flow of time, everything just is. Nonetheless, we do live in a world where time does flow. We’re bound to experience time one moment after another. To us, the future is undecided, and the past is gone forever. Only the present matters.

Our decisions, actions, and possibilities have not been decided yet. For a being in the fourth dimension, everything already is. But, inside time, we live those choices one decision at a time. The future still hasn’t been decided and our actions do matter.

The Strange Climb Continues

Now that we are confused about understanding the fourth dimension, why not continue to even higher dimensions! Some theories—such as string theory and M-theory—suggest that reality has more than four dimensions. In fact, the universe can have beyond ten dimensions! These extra dimensions help explore the boundaries of physics and make our equations work. They help unify the fundamental forces of nature and explain why particles behave the way they do.

If the fourth dimension is an extension of three dimensions into time, then what extends time? For the 5th dimension, instead of a single world line, reality would include every possible branch of that world. Every choice, every quantum event, all possibilities exist. A five-dimensional being would perceive every versions of you simultaneously. Every possible choice you made, every random event that dictated your life, this fifth dimensional being would see all these versions of you. This theory is what is known as parallel universes.

For the 6th dimension, we extend possibilities to the laws of physics themselves. This 6th dimensional being would perceive every possible universe with every possible laws of physics. Gravity might be stronger. Atoms may behave differently. These would be all possible universes with all possible rules and laws that can dictate a universe.

We can continue but we enter territory so abstract that I believe language would begin to fail. However, we can notice that these theories of extension are realms representing possibilities of possibilities. But, as we did with geometric shapes, we duplicated, extended perpendicularly, and connected (in one way or another).

As we see with these theories, even though our intuition fails, mathematics remains perfectly stable. Mathematics doesn’t care how many axes we add to the equations. Our minds may struggle, but equations remain precise and clear.

Mathematics vs. Imagination

Physics doesn’t help us answer any of these questions since its theories work well with both eternalism and presentism. Based on the perspective, we can make the equation work. However, it brings us to an important question: what is real, the limits of our mind or the limitlessness of mathematics?

Our imagination is powerful, yet limited by the world we evolved in—our three dimensional world. We can use analogies like Flatland to help use better comprehend. These analogies help us stretch our intuition just enough to glimpse beyond the veil. Mathematics, on the other hand, is free. It doesn’t care if we’re talking about four dimensions or forty. It moves effortlessly where we struggle to take even one mental step.

So, let’s ask an important question: which one is more real? The world we imagine or the world equations describe? Are higher dimensions truly out there, shaping reality beyond our senses? Or are they elegant scaffolds of thought—tools that help us describe theories, but that don’t exist beyond the page?

The truth is, we don’t know. But uncertainty is part of the adventure. It’s what drives science forward. Visualization isn’t just curiosity, it’s how we reach toward the edges of knowledge. It’s the bridge between what we can know and what might be true. The universe is stranger, and more beautiful, than anything we can see or imagine.